今回の記事は「アルファベータ(α-β)法」とは何かに関して、最も簡単に解説を行っていく記事になります。初心者にも分かりやすいようにできるだけ簡単に記事を記載していくので是非参考にしてみてください。
機械学習における「アルファベータ(α-β)法」とは?
アルファベータ法は「完全情報零和ゲーム」向きの探索手法の「ミニマックス法」を効率的に行うための手法のことを指します。
「完全情報零和ゲーム」は自身が知らない情報が存在しないゲームのことです。例えばオセロ、将棋などです。運の要素のある、「ババ抜き」「ビンゴ」などはこのゲームから外れます。
では実際にこのアルファベータ法はミニマックス法を効率的に行うための手法ですのでミニマックス法の理解ができていない方はまずは下記の記事からミニマックス法に関して知っておきましょう。
簡単に説明すると下記のようなゲーム木(ゲームの始まりの盤面から終わりまでを図にした)下記のような図でよりよい選択をするアルゴリズムをミニマックス法と言います。
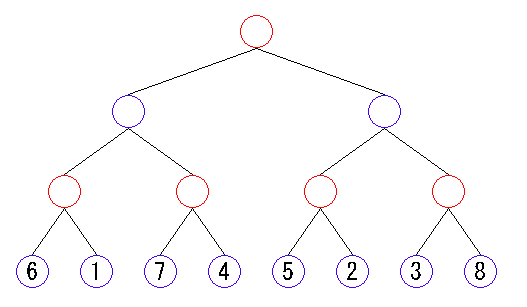
この木の分岐点を接点、またはノードといいます。子ノードがないノードは葉、ノード以下の分岐を枝といいます。
この木の探索を全て行っているとかなり時間を要することが想像できますが、アルファベータ法で枝をカットする手法があり、これで探索にかかる時間を削減できます。
ではそのアルファベータ法に関して詳しく解説していきます。
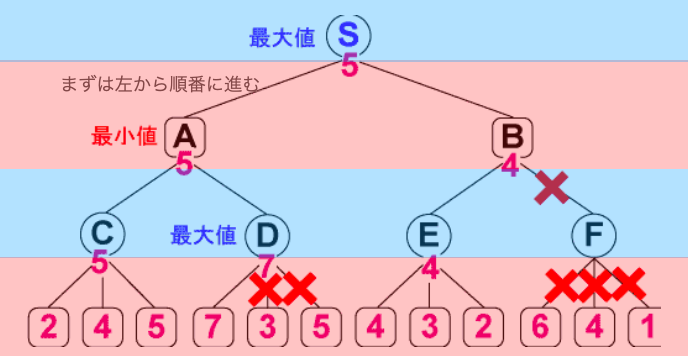
ゲームが最高点を目指す場合
①SからA→Cの順番で相手が何を選ぶかを考える。
②左から順番に2,4,5となっているので最高手は「5」となります。
③つまりCを自身が選択した場合の手は「5」といえます。
④では次にDの手に進みます。
⑤最も左のものが運よく「7」のためこの手はCの手よりも良い手であるとわかる。
⑥この場合Dの続き3,5を探索する必要はなくなるのでこの枝をカットします。
このカットが「αカット」です。
逆に最低点を目指す場合は上記の流れの逆で探索で出てきた最小値以下の枝をカットする手法を「βカット」といいます。
αがそれまでに発見した自身で最も大きな評価値
βがそれまでに発見した相手側で最も小さいもの
では今回の記事は以上です。他にも多数の機械学習関連の記事を記載しているので是非参考にして見て下さい。

コメント